Hexapod

RoboSpider Generation III

Microcontroller:
   PIC18F4550 - Control for 18 Servo Motors

Sensors:
   none - still to do...

Actors:
   12x Modellcraft RS-2
   6x Modellcraft MC 7724 MG
Video:
   First function test

» The basis for this hexapod is the Phoenix hexapod from Lynxmotion. It has a three degrees of freedom leg design so that 18 servo motors need to be controlled. This picture shows the assembly of the legs.


» For controlling the robot I want to use a PIC18F4550 for which I made corresponding PCBs that are tailored to the design of the hexapod. It consists of two parts. One PCB contains the PIC and its own 5V power supply and the other the servo connectors plus the 5V servo power supply. The advantage of this design is that there is less noise the servos cause exposed to the voltage of the microcontroller and any of the two boards can be replaced by a new PCB without the need to build the whole system new.


» This picture shows the installed PCB that fits nicely into the chassis.


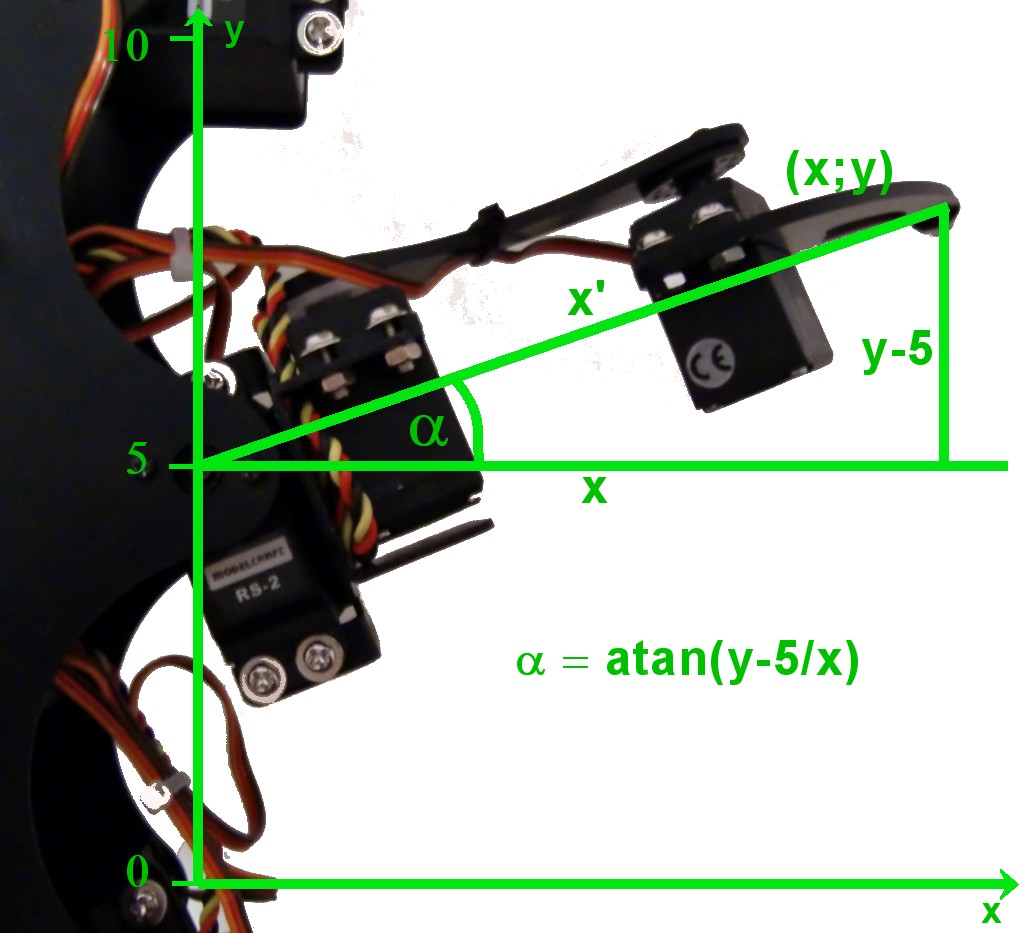» In order to be able to change the height of the spider while it is walking the servo positions for walking shall not be hardcoded but rather be calculated dynamically. This means that (considering a single leg) the position of the end of the leg in form of a x;y;z coordinate shall be given and translated on-the-fly to positions for the three servos of the leg so that the end of the leg reaches the coordinate position.
First of all the angles of each servo to reach the coordinate need to be calculated. These can than be calculated to absolute servo positions. For being able to calculate the servo angles a geometrical model of the spider needs to be made. For the horizontal servo this model is shown in the above picture. Seen from the top, the y axis is pointing from the rear of the spider to the front and the x axis is pointing to the right. The values are in centimeters. I just defined that the leg of the spider can move 5 centimeters for and back. So the servo is at 5 cm. I did not use negative values for the ease of computation in the PIC microcontroller. Maybe I will change this later for being not limited to the 10cm overall range.
So for a position (x;y) we can calculate the servo angle alpha by using arctan.
x' is calculated using the pythagorean theorem (x' = sqrt(x^2 + (y-5)^2)) and is needed for the next step shown below.


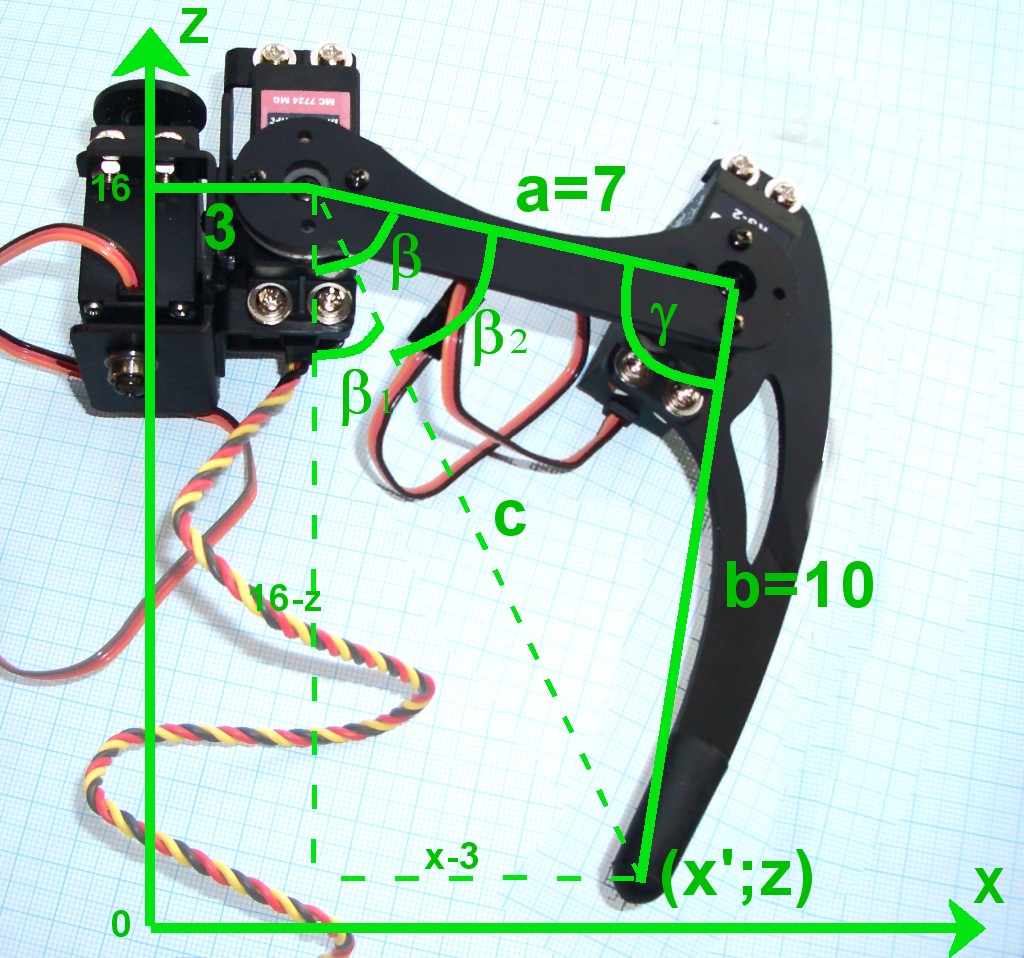» For the vertical leg positioning (along the z-axis) things are getting more complicated. But let's see...
First of all you may notice that the value x' is not neccessarily the x value of the coordinate because if y is not equal to 5 the leg is not parallel to the x-axis so the end of the leg is more distant from the mounting point than x (see picture of horizontal movement). But we have calculated x' already above.
Let's start with the calculation of the angle beta (for servo 2) which is the sum of beta1 + beta2:
  • beta1 = atan((x'-3)/16-z)
  • beta2 = acos((b^2-d^2-c^2)/-2*d*c)
c, again, can be calculated using the pythagorean theorem (x' = sqrt((x'-3)^2 + (16-z)^2))

To be continued....